Cette fiche introduit la notion d'arbre binaire de recherche et une implantation en langage C.

Il est essentiel d'avoir lu la fiche sur les Structures arborescentes, en particulier la section sur les arbres binaires, avant d'aborder celle-ci.

1. Introduction

Un arbre binaire de recherche (ABR) ou Binary Search Tree (BST) est un type particulier d'arbre binaire dont les nœuds respectent récursivement la propriété d'ordre suivante. Pour chaque nœud n :

  • Les étiquettes du fils gauche sont inférieures ou égales à l'étiquette du nœud n
  • les étiquettes du fils droit droit sont supérieures à l'étiquette du nœud n

Il en résulte que pour un nœud n l'ensemble du sous-arbre gauche contient des étiquettes inférieures ou égales à celle de n et que l'ensemble du sous-arbre droit contient des étiquettes supérieures à celle de n.

Ainsi, l'arbre suivant est un BST :

tandis que celui ci dessous n'en est pas un :

2. Intérêt des BST

Cet ordonnancement imposé assure que les opérations d'ajout, de recherche et de suppression se font en un temps moyen rapide. Cependant, nous verrons que les données ont un impact important sur la structure de l'arbre et sur ses performances.

Le BST est particulièrement adapté à la représentation des ensembles ordonnés (au sens mathématique du terme). Il peut également être utilisé pour trier des données (mais de manière inefficace) et pour représenter des files de priorité.

3. Définition du type abstrait "Bst"

D'un point de vue abstrait, un BST est un arbre binaire, il est donc défini par soit :

  • un arbre vide ;
  • Un nœud (racine) et au plus 2 sous-arbres dont le gauche (resp. droit) contient des étiquettes < (resp. >) à l'étiquette du nœud.

Un BST n'accepte que des étiquettes que l'on peut comparer et sur lesquelles on peut effectuer un tri. En pratique, les éléments constituant les étiquettes doivent donc être fournis avec une fonction de comparaison de deux éléments.

Tout comme les arbres binaires, le BST étant une structure récursive, les algorithmes applicables au BST sont donc eux-mêmes des algorithmes utilisant la récursivité.

Les opérations de base sur les BST sont les suivantes :

  • Créer un BST vide
  • Tester si un BST est vide
  • Recherche un noeud dans le BST
  • Ajouter un nœud au BST
  • Supprimer un nœud du BST
  • Afficher le BST

La suite de la fiche présente les différents outils sur les BST.

4. Le TAD bst_t

Un bst est :

  • soit vide
  • soit un triplet "root, B1, B2" où root est un nœud et B1 et B2 sont deux arbres binaires disjoints.

Les nœuds d'un arbre binaire comportent 0,1 ou 2 fils.

4.1 Définition des types

Les étiquettes sont de type element_t.

Les nœuds et les arbres sont définis par les types node_t et bst_t

Un bst est une structure comportant des nœuds avec 3 champs contenant chacun une étiquette et les sous arbres fils du nœud : 


            typedef int element_t;

            typedef struct _node{
              element_t value;
              struct _node* left;
              struct _node* right;
            } node_t, *bst_t;

ou encore plus simple : 

            typedef binarytree_t bst_t;

Interface minimale en C du type abstrait des bst :

prototype contrat
bst_t bst_new() crée et retourne un bst vide ;
int bst_is_empty() retourne 1 si l'arbre est vide, 0 sinon ;
int bst_lookup(element_t val,bst_t arbre) Recherche le nœud dont étiquette est le paramètre val
Retourne vrai si le nœud contenant cette valeur est dans l'arbre ou faux sinon ;
bst_t bst_insert(element_t val,bst_t arbre) crée un nouveau nœud dont étiquette est le paramètre val, et qui sera placé de façon à respecter les contrainte du BST.
retourne l'arbre dans lequel le nœud a été ajouté ou l'arbre non modifié si l’élément n'a pas sa place dans l'arbre ;
bst_t bst_node_del(element_t val,bst_t arbre) supprimer le nœud dont l'étiquette est le paramètre val
retourne l'arbre dans lequel le nœud a été supprimé ou l'arbre non modifié si l’élément n'était pas présent ;
bst bst_delete(bst_t arbre) libère la mémoire de tous les nœuds de l'arbre arbre et retourne un arbre vide ;
void bst_print(bst_t arbre) affiche tous les nœuds de l'arbre arbre ;

5. Les parcours sans modification dans un bst_t

5.1 La recherche d'un élément dans un bst_t

La recherche dans un bst s'effectue typiquement de manière récursive. En partant de la racine, la valeur recherchée est comparée au nœud. Si la valeur est plus petite, la recherche est relancée sur le sous arbre gauche. Si elle est plus grande elle est relancée sur le sous-arbre droit.

En terme de complexité, la recherche dans un bst peut être comparée à la recherche par dichotomie.

Quelle est la complexité de cette fonction recherche sur l'arbre ci dessous ?

Soit l'arbre suivant :

et le code suivant : 


  #include "bst.h"

  int bst_lookup(element_t val,bst_t root) {
    if (!binarytree_is_empty(root)) {
      if (compare(val,root->value)==0)
      return 1;
      else if (compare(val,root->value)<0)
      return bst_lookup(val,root->left);
      return bst_lookup(val,root->right);
    }
    return O;
  }

  int main() {
    bst_t mytree;
    mytree = ...
    int found = bst_lookup(12,mytree);
  }
Quel est la complexité de cette recherche dans le pire des cas?

O(n) NON, car on ne parcours qu'une branche de l'arbre. On a donc pas besoin de parcourir tous les nœuds. O(log(n)) GAGNE O(n2) NON, car on ne parcours qu'une branche de l'arbre. On a donc pas besoin de parcourir tous les nœuds.

5.2 Affichage trié

On peut réaliser l'affichage par ordre croissant d'un arbre binaire de recherche en utilisant le parcours infixe. Autrement dit, on peut reprendre la fonction de l'arbre binaire et l'appliquer au BST.

Quel est le résultat de cette fonction print sur l'arbre ci dessous ?

Soit la fonction suivante que l'on applique à l'arbre suivant : 


              #include "binarytree.h"

              void bst_print(bst_t root) {
                if (!bst_is_empty(root)) {
                  bst_print(root->right);
                  element_print(root->value);
                  bst_print(root->left);
                }
              }
Quel est le résultat de l'affichage ? t q l i g e d a ? OUI, c'est un affichage par ordre décroissant. dans le parcours préfixe il suffit d’intervertir branche droite et gauche a d e g i l q t ? NON, oups cette fonction ne marche pas comme elle devrait e a i d g t q l ? NON, cet affichage correspond à un parcours en largeur d'abord e a q i g t q l ? NON, ca c'est le parcours préfixe

6 parcours avec modification d'un bst_t

6.1 Insertion d'un élément dans un bst_t

Tout élément ajouté à l'arbre doit respecter la notion d'arbre binaire de recherche. On doit donc parcourir l'arbre pour trouver l'emplacement idéal de l’élément à insérer, créer le noeud et l'inserer dans l'arbre original. On distingue 2 cas :

  • si l'arbre est vide alors
    • créer un nœud et le retourner ce nœud.
  • sinon
    • si la valeur stockée sur la racine est plus grande que la valeur à insérer, alors ajouter ce nœud dans le sous arbre gauche et retourner le nouvel arbre
    • sinon ajouter ce nœud dans le sous arbre droit et retourner le nouvel arbre.

Exemple d'insertion dans un BST 

                bst_t bst_insert(element_t val,bst_t tree){
                  if (!bst_is_empty(tree)) {
                    /*si l'arbre n'est pas vide on cherche la branche à parcourir*/
                    if (val < tree->val)
                    tree->left=bst_insert(val,tree->left);
                    else
                    tree->right=bst_insert(val,tree->right);
                  }
                  else {
                    /* dès que l'arbre est vide on retourne un nouvel arbre qui inclut l'élément */
                    tree =(bst_t) calloc(1,sizeof(*bst_t));
                    tree->val=val;
                  }
                  return tree;
                }

                int main() {
                  bst_t mytree=bst_new();
                  mytree=bst_insert(60,mytree);
                  mytree=bst_insert(90,mytree);
                  mytree=bst_insert(30,mytree);
                  mytree=bst_insert(50,mytree);
                }

arbre vide : insertion de 60

On entre dans la fonction et on teste si l'arbre est vide.

On créé le nouveau nœud.

on stocke la valeur.

On sort de la fonction et on retourne le nouvel arbre de racine 60

insertion de 90

On entre dans la fonction et on teste si l'arbre est vide.

90 n'est pas inférieur à 60

on entre donc dans le else

Puis on relance l'insertion de 90 sur l'arbre droit

On entre dans la fonction et on teste si l'arbre est vide.

On créé le nouveau nœud.

on stocke la valeur.

On sort de la fonction et on retourne le nouvel arbre de racine 90

On récupère le nouvel arbre droit en le raccrochant à la racine

On sort de la fonction et on retourne le nouvel arbre de racine 60

insertion de 30

On entre dans la fonction et on teste si l'arbre est vide.

30 est inférieur à 60

Puis on relance l'insertion de 30 sur l'arbre gauche

On entre dans la fonction et on teste si l'arbre est vide.

On créé le nouveau nœud.

on stocke la valeur 30.

On sort de la fonction et on retourne le nouvel arbre de racine 30

On récupère le nouvel arbre gauche en le raccrochant à la racine

On sort de la fonction et on retourne le nouvel arbre de racine 60

insertion de 50

On entre dans la fonction et on teste si l'arbre est vide.

50 est inférieur à 60

Puis on relance l'insertion de 50 sur l'arbre gauche

On entre dans la fonction et on teste si l'arbre est vide.

50 n'est pas inférieur à 30

on entre donc dans le else

Puis on relance l'insertion de 50 sur l'arbre droit

On entre dans la fonction et on teste si l'arbre est vide.

On créé le nouveau nœud.

on stocke la valeur 50.

On sort de la fonction et on retourne le nouvel arbre de racine 50

On récupère le nouvel arbre droit en le raccrochant à la racine de 30

On sort de la fonction et on retourne le nouvel arbre de racine 30

On récupère le nouvel arbre gauche en le raccrochant à la racine

On sort de la fonction et on retourne le nouvel arbre de racine 60

On sort du programme en ayant bien construit un BST

6.2 Suppression d'un élément dans un bst_t

Supprimer un élément d'un arbre binaire de recherche n'est pas aussi simple que d'en insérer un. En effet, contrairement à l'insertion qui ne s'effectue qu'au niveau des feuilles, une suppression peut être appliquée à n'importe quel nœud (racine, nœud intermédiaire ou feuille). Par ailleurs, si l'insertion consiste à ajouter un fils à un père, la suppression d'un père nécessite de raccrocher deux fils à l'arbre, tout en respectant les contraintes du BST...

Comment choisir le nœud qui remplacera le nœud supprimé ?

Dans l'exemple ci-dessous, le nœud 30 est supprimé. Quel nœud doit être choisi pour le remplacer ? Donner la loi de remplacement du cas général pour assurer que le nœud remplacé respecte les contraintes du BST.

Il suffit de prendre le fils de droite (il est forcement supérieur au fils gauche) NON, car que fait-on du fils gauche ? Où le raccroche-t-on si le fils droit a déjà deux fils? Il suffit de prendre la feuille la plus à gauche du fils droit OUI car c'est le minimum des valeurs supérieures à 30. On est donc assuré que la branche de droite ne contient que des éléments supérieurs et que la branche de gauche ne contient que des éléments inférieurs. Les contraintes du BST sont respectées. Il suffit de prendre la feuille la plus à droite du fils gauche OUI car c'est le maximum des valeurs inférieures à 30. On est donc assuré que la branche de droite ne contient que des éléments supérieurs et que la branche de gauche ne contient que des éléments inférieurs. Les contraintes du BST sont respectées. Il suffit de prendre le fils de gauche (il est forcement inférieur au fils droit) NON, car que fait-on du fils droit ? Où le raccroche-t-on si le fils gauche a déjà deux fils?

Pour supprimer un nœud de valeur val il y a donc un choix à effectuer dans le cas général. Sinon on distingue plusieurs cas :

  • si l'arbre est vide alors on retourne un arbre vide.
  • sinon si val < à la racine, le fils gauche devient le résultat de la suppression sur le fils gauche
  • sinon si val > à la racine, le fils droit devient le résultat de la suppression sur le fils droit
  • sinon si val == à la racine alors
    • s'il n'y a pas d'enfant, on supprime le nœud et on retourne vide
    • s'il y a un seul enfant à gauche (resp. droite) on supprime le nœud et on retourne le fils gauche (resp. droit)
    • sinon on retire le plus grand nœud du fils gauche et on le stocke à la place de la racine, puis on retourne cette nouvelle racine.


bst_t bst_node_del(element_t val, bst_t tree) { /* val à supprimer */
  if (bst_is_empty(tree))
    return tree; /* arbre vide : pas de suppression */
  else if (val < tree->val) {
    tree->left=bst_node_del(val, tree->left);
    return tree;
  }
  else if (val > tree->val){
    tree->right =bst_node_del(val, tree->right );
    return tree;
  }
  else if (!tree->left) {  /* c’est le nœud a supprimer */
    if (!tree->right) {
       /* Aucun fils */
      free(tree);
      return(NULL);
    }
    else
    {
      /*1 fils droit*/
      bst_t q=tree;
      tree=tree->right;
      free(q);
      return tree;
    }
  }
  else if (!tree->right)  {
    /*1 fils gauche*/
    bst_t q=tree;
    tree=tree->left;
    free(q);
     return tree;
   }
  else{
    /*2 fils*/
    tree->left= SupMax(tree,tree->left) ;
     return tree;
   }
}


bst_t SupMax(bst_t dep, bst_t p){
  /* dep : nœud à supprimer
  recherche la valeur la plus grande du sous arbre gauche (=Max)
  recopie dans le nœud dep ce Max,  détruit le nœud où se trouve ce Max
  retourne le nouveau sous-arbre ainsi modifié
  */

	if (!p->right) {  /* Max trouve */
			bst_t q ;
      dep->val=p->val ; /* recopie de la valeur Max */
      q = p->left ;  free(p) ;   return q;    /* nouveau SAG */
  }
  else {
		p->right = SupMax(dep,p->right) ; return p ;
  }
}

7 Performance et équilibrage des arbres binaires de recherche

7.1 Dépendance aux données

La forme de l'arbre binaire de recherche tel que nous l'avons vu est très dépendante de la manière dont les données sont insérées.

Quel forme d'arbre obtient on avec le code suivant? 


    int main (){
      bst_t tree = bst_new();
      int i;
      for (i=0;i<20;i++) {
        tree = bst_insert(i,tree);
      }
      bst_print(tree);
    }

NON, ça sent la réponse au hasard...

OUI car tout les éléments étant ajoutés par ordre croissant, il vont tous se retrouver en tant que fils droit pour prendre cette forme de peigne.

NON car tout les éléments étant ajoutés par ordre croissant, il vont tous se retrouver en tant que fils droit pour prendre une forme de peigne.

NON, ça sent la réponse au hasard...

La complexité du BST étant dépendante de la hauteur h de l'arbre, plus l'arbre a une forme de peigne plus h augmente et moins la recherche dans le BST devient efficace. On dit que l'arbre est déséquilibré. Idéalement, h devrait être aussi petit que possible, ce qui arrive lorsque l'arbre est complet (h=log(n)). Dans ce cas, on dit que l'arbre est équilibré.

7.2 Vers une forme parfaite (ou presque) ?

Maintenir un arbre complet a un coût. Maintenir l'équilibre est trop lourd en recopie/déplacement d'éléments. Par exemple, l'ajout de l'élément 1 dans le BST ci-dessous implique le déplacement de l'ensemble des éléments.

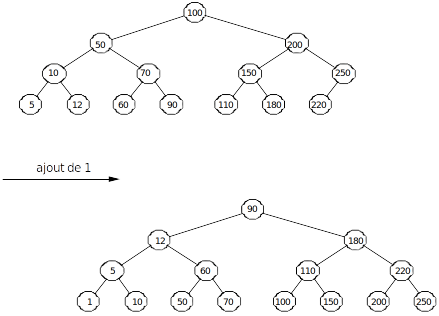
Pour parvenir à une solution satisfaisante, une idée consiste à relaxer la contrainte de l’équilibre afin d'obtenir des arbres presque parfaits. Dans ce cas, on définit le facteur d'équilibrage comme la hauteur de son sous-arbre gauche moins celle de son sous-arbre droit. Si le facteur a une valeur de -1, 0 ou 1. Alors il est considéré comme équilibré.

Ce facteur a été utilisé pour construire des BST automatiquement équilibrés. On peut notamment citer les arbres AVL du nom de leurs auteur Georgii Adelson-Velsky et Evguenii Landis. Dans leur algorithme, toutes les opérations d'insertion, de suppression et de recherche s'effectuent en O(log(n)) tous en conservant un BST ayant un facteur d'équilibrage entre -1 et 1.

Pour cela, les auteurs utilisent le mécanisme de rotation qui permet de modifier la hauteur d'un fils gauche (resp. droit) au détriment du fils droit (resp. gauche) sans violer les contraintes du BST.

Dans les BST, une rotation s'effectue en échangeant un père et son fils droit (rotation à gauche) ou son fils gauche (rotation à droite). Dans l'exemple ci-dessous, dans le cas d'une rotation à droite, 50 (racine) et 30 (fils gauche) sont échangés. Le fils droit de 30 (ici 40) devient le fils gauche de 50 car on est assuré, par construction, qu'il est inférieur à 50. Les contraintes du BST sont donc conservées dans les rotations.

Dans l'algorithme AVL, à chaque insertion ou suppression, le facteur équilibre est calculé et des rotations sont effectuées pour corriger le déséquilibre. La figure ci-dessous montre comment ces rotations peuvent corriger le facteur d'équilibre pour un arbre simple. Dans l’algorithme AVL, chaque insertion va provoquer jusqu'à une rotation. La suppression consiste à faire descendre le nœud à supprimer sur une feuille, la supprimer, puis à corriger le facteur équilibre (en, au plus, h rotations). Le maintien de l'équilibre ne modifie donc pas la complexité des fonctions d'insertion et de suppression du BST tout en assurant une structure d'arbre quasi-parfaite.

Beaucoup d'autres algorithmes existent tels que les arbres 2-3 ou les arbres B qui maintiennent un équilibre en faisant varier le nombre d'étiquettes ou de fils que chaque nœud peut accueillir.