Cette fiche introduit la notion et la réalisation des types abstraits Tree.

Dans cette fiche, on présente le concept d'arbre binaire et les différents parcours permettant d'utiliser les données stockées sur ce type d'arbre.

On présente une implémentation par chaînage.

1. Introduction

Les arbres sont des structures souvent utilisés pour représenter des données. On peut ainsi représenter les résultats d'un tournoi de sport, un livre,

ou des expressions arithmétiques dans un éditeur d'équations. L'expression (9+x)*6 se représente par l'arbre :

2. Terminologie

Un arbre est formé de nœuds. Un nœud contient une information l'étiquette et l'accès aux arbres fils. Les différents types de nœuds sont :

  • la racine : le premier nœud qui donne accès à l'arborescence.
  • les feuilles (= ou nœuds terminaux) : nœuds qui n'ont aucun fils
  • les nœuds internes : nœuds qui ont au moins un fils

En partant de la racine, pour aller vers les feuilles, on parcourt

  • un chemin menant à un nœud : suite des nœuds menant de la racine au nœud concerné
  • une branche : chemin de la racine à une feuille

3. Définition du type abstrait "Tree"

D'un point de vue abstrait, un arbre est soit :

  • un arbre vide ;
  • Un noeud racine et des sous-arbres qui sont ses fils.

Un arbre est donc fondamentalement une structure récursive et ne peut pas se traiter de manière itérative (au contraire des listes par exemple). La plupart des algorithmes seront donc des algorithmes utilisant la récursivité.

Les opérations de base sur les arbres sont les suivantes :

  • Créer un arbre vide
  • Tester si un arbre est vide
  • Construire un arbre formé par un nœud (la racine) et ses fils
  • Obtenir les fils

Pour utiliser les arbres, il faut pouvoir parcourir les nœuds de l'arbre. 2 grands types de parcours :

  • Parcours en largeur : on examine les nœuds du premier niveau, puis tous ceux du deuxième niveau, puis tous ceux du troisième niveau, etc...
  • Parcours en profondeur : on examine la racine, puis le premier fils de la racine, puis le premier fils du premier fils de la racine etc..

La suite de la fiche présente les différents outils sur les arbres binaires.

4. Le TAD binarytree_t

Un arbre binaire est

  • soit vide
  • soit un triplet "root, B1, B2" où root est un nœud et B1 et B2 sont deux arbres binaires disjoints.

Les nœuds d'un arbre binaire comportent 0,1 ou 2 fils.

Pour définir les nœuds d'un arbre binaire, nous avons besoin de 3 informations :

  • l'étiquette qui contient les informations utiles
  • l'adresse du fils gauche
  • l'adresse du fils droit

4.1 Définition des types

Les étiquettes sont de type element_t.

Les nœuds et les arbres sont définis par les types node_t et binarytree_t

Un arbre est une structure comportant des nœuds avec 3 champs contenant chacun une étiquette et les sous arbres fils du nœud : 


            typedef int element_t;

            typedef struct _node{
              element_t value;
              struct _node* left;
              struct _node* right;
            } node_t, *binarytree_t;

Interface minimale en C du type abstrait des arbres binaires :

prototype contrat
binarytree_t binarytree_new() crée et retourne un arbre vide ;
binarytree_t binarytree_is_empty() retourne 1 si l'arbre est vide, 0 sinon ;
binarytree_t binarytree_add_root(element_t val,binarytree_t fg, binarytree_t fd) crée un nouveau nœud dont l'étiquette est le paramètre val, dont le fils gauche sera le paramètre fg et dont le fils droit sera le paramètre fd.
retourne l'arbre formé par ce nœud ;
binarytree_t binarytree_node_del(element_t val,binarytree_t arbre supprimer le nœud dont l'étiquette est le paramètre val
retourne l'arbre résultat ;
binarytree_t binarytree_search(element_t val,binarytree_t arbre Recherche le nœud dont l'étiquette est le paramètre val
Retourne le nœud contenant cette valeur ou NULL sinon ;
binarytree_t binarytree_delete(binarytree_t t) libère la mémoire de tous les nœuds de l'arbre t et retourne un arbre vide ;

5. Les parcours d'un arbre binarytree_t

Pour utiliser les informations contenues dans l'arbre, il faut parcourir les nœuds en partant de la racine.

2 type de parcours sont utilisés : en profondeur ou en largeur selon les algorithmes.

5.1 Les parcours en profondeur binarytree_t sans modification de l'arbre

L'exemple type est l'affichage des nœuds de l'arbre. La fonction est une fonction récursive dont l'algorithme est très simple. Si l'arbre n'est pas vide, il faut simplement afficher :
  • le contenu de la racine
  • afficher le sous arbre gauche
  • afficher le sous arbre droit
sinon il ne faut rien faire

L'ordre de ces 3 étapes peut être modifié et donne un ordre de parcours différents.
On dispose ainsi des parcours préfixé, infixé et postfixé aussi appelés RacineGaucheDroit (RGD), GaucheRacineDroit (GRD) et GaucheDroitRacine (GDR).

5.1.1 Parcours préfixé


Pendant le parcours préfixé, on agit (ici, on affiche) d'abord le nœud racine avant de traiter de la même manière (récursivement) le sous arbre gauche puis le sous arbre droit.

Quel est le résultat de cette fonction print sur l'arbre ci dessous ?

Soit l'arbre suivant

et le code suivant 


            #include "binarytree.h"

            void binarytree_print_prefixe(binarytree_t root) {
              if (!binarytree_is_empty(root)) {
                element_print(root->value);
                binarytree_print_prefixe(root->left);
                binarytree_print_prefixe(root->right);
              }
            }

            int main() {
              binarytree_t mytree;
              mytree = binarytree_add_root(0,
                          binarytree_add_root(1,
                            binarytree_add_root(3,
                              binarytree_add_root(7,NULL,NULL),
                              binarytree_add_root(8,NULL,NULL)),
                            binarytree_add_root(4,
                              binarytree_add_root(9,NULL,NULL),
                              binarytree_add_root(10,NULL,NULL)),
                          binarytree_add_root(2 ....)));
              binarytree_print_prefixe(mytree);
            }
Quel est le résultat de l'affichage ? 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ? NON, on affiche le sous arbre gauche du nœud 1 avant d'afficher le nœud 2. Donc on affiche d'abord la racine (0), puis son fils gauche(1), puis son petit fils gauche (3) 0 1 3 7 8 4 9 10 2 5 11 12 6 13 14 ? GAGNE 7 8 9 10 11 12 13 14 15 3 4 5 6 1 2 0 ? NON, on affiche le sous arbre gauche du nœud 1 avant d'afficher le nœud 2. Donc on affiche d'abord la racine (0), puis son fils gauche(1), puis son petit fils gauche (3)

Comment se déroule cette fonction ?

Exemple de parcours prefixé 

                void binarytree_print_prefixe(binarytree_t root) {
                  if (!binarytree_is_empty(root)) {
                    element_print(root->value);
                    binarytree_print_prefixe(root->left);
                    binarytree_print_prefixe(root->right);
                  }
                }

                int main() {
                  binarytree_t mytree;
                  mytree = .....;
                  binarytree_print_prefixe(mytree);
                }

racine de l'arbre : 0

On affiche la racine (0)

On appelle la fonction sur le sous arbre gauche.

On affiche la racine (1)

On appelle la fonction sur le sous arbre gauche.

L'arbre est le sous arbre gauche de 1

On affiche la racine (3)

On appelle la fonction sur le sous arbre gauche de 3

Le sous arbre gauche de 3 est vide

L'arbre est vide, le test n'est pas vérifié

Fin de la fonction qui affiche le sous arbre gauche de 3; Retour à la fonction qui affiche l'arbre de racine 3.

On appelle la fonction sur le sous arbre DROIT de 3

Le sous arbre droit de 3 est vide

L'arbre est vide, le test n'est pas vérifié

Fin de la fonction qui affiche le sous arbre droit de 3; Retour à la fonction non terminée qui affiche l'arbre de racine 3.

On a terminé l'affichage du nœud 3

Fin de la fonction d'affichage du nœud 3,
Retour à la fonction non terminée qui affiche l'arbre de racine 1.

On est de retour ici, apres avoir affiché le sous arbre gauche de 1.

On appelle la fonction sur le sous arbre DROIT de 1

Le sous arbre droit de 1 est :

On affiche la racine (4)

On appelle la fonction sur le sous arbre gauche de 4

le sous arbre gauche de 4 est vide

L'arbre est vide, le test n'est pas vérifié

Fin de la fonction, retour à la fonction non terminée affiche l'arbre de racine 4.

On appelle la fonction sur le sous arbre DROIT de 4

Le sous arbre droit de 4 est vide

L'arbre est vide, le test n'est pas vérifié

Fin de la fonction qui affiche le sous arbre droit de 4; Retour à la fonction non terminée qui affiche l'arbre de racine 4.

On a terminé l'affichage du nœud 4

Fin de la fonction d'affichage du nœud 4,
Retour à la fonction non terminée qui affiche l'arbre de racine 1.

On a terminé l'affichage du nœud 1

Fin de la fonction, retour à la fonction non terminée qui affiche l'arbre de racine 0. etc........

5.1.2 Parcours infixé


Pendant le parcours infixé, on traite (ici, on affiche) d'abord (récursivement) le sous arbre gauche puis on agit sur le nœud racine avant de traiter le sous arbre droit.

Quel est le résultat de cette fonction print sur l'arbre ci dessous ?

Soit l'arbre suivant

et le code suivant 


            #include "binarytree.h"

            void binarytree_print_infixe(binarytree_t root) {
              if (!binarytree_is_empty(root)) {
                binarytree_print_infixe(root->left);
                element_print(root->value);
                binarytree_print_infixe(root->right);
              }
            }

            int main() {
              binarytree_t mytree;
              mytree = binarytree_add_root(0,
                          binarytree_add_root(1,
                            binarytree_add_root(3,
                              binarytree_add_root(7,NULL,NULL),
                              binarytree_add_root(8,NULL,NULL)),
                            binarytree_add_root(4,
                              binarytree_add_root(9,NULL,NULL),
                              binarytree_add_root(10,NULL,NULL)),
                          binarytree_add_root(2 ....)));
              binarytree_print_infixe(mytree);
            }
Quel est le résultat de l'affichage ? 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ? NON, on affiche d'abord le sous arbre gauche du nœud 0 avant d'afficher le nœud 0. Donc on affiche d'abord le sous arbre fils gauche commençant par 1, puis le nœud 0 puis son sous arbre fils droit (2) 0 1 3 7 8 4 9 10 2 5 11 12 6 13 14 ? NON, on affiche d'abord le sous arbre gauche du nœud 0 avant d'afficher le nœud 0. Donc on affiche d'abord le sous arbre fils gauche commençant par 1, puis le nœud 0 puis son sous arbre fils droit (2) 7 3 8 1 9 4 10 0 11 5 12 2 13 6 14 ? GAGNE 7 8 9 10 11 12 13 14 15 3 4 5 6 1 2 0 ? NON, on affiche d'abord le sous arbre gauche du nœud 0 avant d'afficher le nœud 0. Donc on affiche d'abord le sous arbre fils gauche commençant par 1, puis le nœud 0 puis son sous arbre fils droit (2)

5.1.3 Parcours postfixé


Pendant le parcours postfixé, on traite (ici, on affiche) d'abord (récursivement) le sous arbre gauche avant de traiter le sous arbre droit. puis on agit sur le nœud racine

Quel est le résultat de cette fonction print sur l'arbre ci dessous ?

Soit l'arbre suivant

et le code suivant 


            #include "binarytree.h"

            void binarytree_print_postfixe(binarytree_t root) {
              if (!binarytree_is_empty(root)) {
                binarytree_print_postfixe(root->left);
                binarytree_print_postfixe(root->right);
                element_print(root->value);
              }
            }

            int main() {
              binarytree_t mytree;
              mytree = binarytree_add_root(0,
                          binarytree_add_root(1,
                            binarytree_add_root(3,
                              binarytree_add_root(7,NULL,NULL),
                              binarytree_add_root(8,NULL,NULL)),
                            binarytree_add_root(4,
                              binarytree_add_root(9,NULL,NULL),
                              binarytree_add_root(10,NULL,NULL)),
                          binarytree_add_root(2 ....)));
              binarytree_print_postfixe(mytree);
            }
Quel est le résultat de l'affichage ? 7 8 3 9 10 4 1 11 12 5 13 14 6 2 0 ? GAGNE 0 1 3 7 8 4 9 10 2 5 11 12 6 13 14 ? NON, on affiche d'abord le sous arbre gauche du nœud 0 puis le sous arbre droit avant d'afficher le nœud 0. Donc on affiche d'abord le sous arbre fils gauche commençant par 1, puis son sous arbre fils droit (2) puis le nœud 0, qui se trouve en dernier. 7 3 8 1 9 4 10 0 11 5 12 2 13 6 14 ? NON, on affiche d'abord le sous arbre gauche du nœud 0 puis le sous arbre droit avant d'afficher le nœud 0. Donc on affiche d'abord le sous arbre fils gauche commençant par 1, puis son sous arbre fils droit (2) puis le nœud 0, qui se trouve en dernier. 7 8 9 10 11 12 13 14 15 3 4 5 6 1 2 0 ? NON, on affiche d'abord le sous arbre gauche du nœud 0 puis le sous arbre droit avant d'afficher le nœud 0. Donc on affiche d'abord le sous arbre fils gauche commençant par 1, puis son sous arbre fils droit (2) puis le nœud 0, qui se trouve en dernier.

5.2 Le parcours en largeur binarytree_t sans modification de l'arbre

L'ordre des nœuds parcourus est maintenant celui des générations : on parcourt d'abord la racine, puis tous les fils de la racine, puis tous les petits fils de la racine, etc...

Pour réaliser ce parcours, une file est obligatoire. Voici l'algorithme de parcours en largeur 


          #include "binarytree.h"

          void binarytree_print_breadth(binarytree_t root) {
            if (!binarytree_is_empty(root)) {
                // Un pointeur pour parcourir les nœuds de l'arbre
              binarytree_t p=binarytree_new();
                // Une file de priorité
              fifo_t myfile=fifo_new();
                // An ajoute la racine à la file
              myfile=fifo_enqueue(root,myfile);
                // tant qu'il y a des nœuds dans la file
              while (!fifo_is_empty(myfile)) {
                p = fifo_dequeue(&myfile);
                  // On traite le nœud
                element_print(p->value);
                  // On enfile le fils gauche
                if (p->left) myfile=fifo_enqueue(p->left,myfile);
                  // On enfile le fils droit
                if (p->right) myfile=fifo_enqueue(p->right,myfile);
                  // On peut bien sur avoir plus de fils
              }
            }

5.3 Les parcours en profondeur binarytree_t AVEC modification de l'arbre

Si l'arbre doit être modifié, par exemple pour ajouter un nœud à l'arbre, l'écriture des fonctions est différente. voici une fonction générique qui donne un exemple d'une fonction parcourant et modifiant l'arbre. Un exemple plus simple sera vu lors de l'ajout d'un nœud dans un arbre binaire de recherche. 


            binarytree_t binarytree_modification(binarytree_t p) {
              if (p) {
          	        /* Je fais ce que je dois faire sur la valeur de ma racine */
                p->val=action(p);

                    /* Si besoin, Je fais ce que je dois faire sur le fils gauche :
          	         Je récupère le nouvel arbre et je change le fils gauche avec
          	         le nouvel arbre */
                p->left=binarytree_modification (p->gauche);

          	     /* Idem pour le droit */
                p->right=binarytree_modification (p->droit);
              }
              else { 
          	    /* Cas ou l’arbre est vide : Peut etre y a t il qqchose à faire ici*/
              }
              return p;
            }

6. Les arbres n-aire

On peut facilement étendre le concept d'arbre binaire vers des arbres à un nombre strictement positif n de fils.

6.1 Arbres n-aire classique

Dans ce cas on peut utiliser une représentation par tableau ou par liste. 


            typedef int element_t;
	    #define N 10
            typedef struct _node{
              element_t value;
              struct _node* sons[N];
            } node_t, *tree_t;
ou encore 

            typedef struct _node{
              element_t value;
              list_t sons;
            } node_t, *tree_t;

Ces arbres n-aires permettent de représenter des données bien plus complexes de manière efficace. Par exemple, dans le cas d'un lexique composé de allez, allons, va, vais, vas, vont, celui-ci peut-être représenté par l'arbre ci-dessous, qui représente tout les chemins possibles (et évite les répétitions de lettres)

6.2 Arbres n-aire par extension des arbres binaires

Afin de réutiliser utilement tous les travaux effectués sur les arbre binaires, on peut utiliser une autre relation familiale (fratrie) pour représenter les arbres n-aire. Ainsi, l'un des fils reste une relation de descendance tandis que l'autre fils devient une relation de fratrie. 


            typedef int element_t;
            typedef struct _node{
              element_t value;
              struct _node* son;
              struct _node* sibling;
            } node_t, *tree_lex_t;

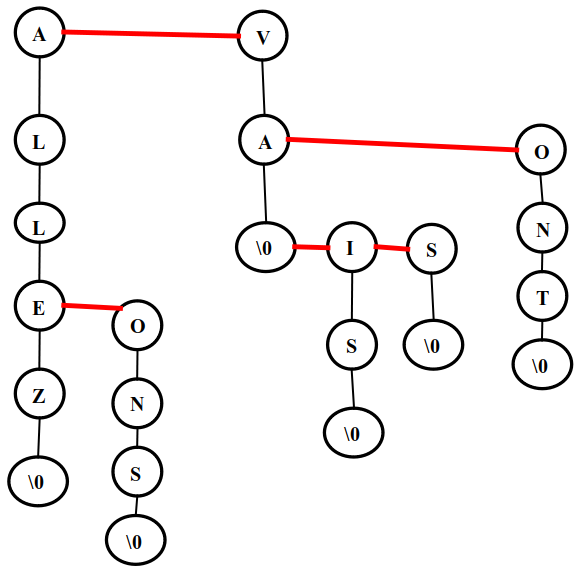
L'arbre ci-dessous reprend les données précédentes mais dans une structure d'arbre binaire de type "fils-frère". Le fils représente une lettre suivante du mot, tandis que le frère représente une lettre de même niveau que le nœud.