Cette fiche introduit la notion et la réalisation du type abstrait HashTable, appelé en Français "Table d'association" ou encore "dictionnaire".
Dans cette fiche, on explicite le concept de la table de Hachage puis pas à pas les points essentiels de l'implémentation.
1. Introduction : de la nécessité des tables
Philibert-Ulbéric, maintenant à la tête d'une liste pour succéder au bureau des élèves, souhaite se faire un annuaire téléphonique de ses coreligionnaires. Il lui faut donc associer un numéro de téléphone à chaque étudiant de Phelma. Analysant ces besoins, il définit ainsi les opérations qu'il doit pouvoir faire sur sa structure de données :
- créer une structure vide,
- ajouter un couple nom-téléphone à la structure,
- retrouver le téléphone à partir d'un nom dans la structure,
- savoir si un couple nom-téléphone appartient à la structure,
- supprimer un couple nom-téléphone de la structure,
- afficher tous les couples nom-téléphone de la structure.
Il est sous-entendu que les opérations doivent être le plus rapide possible, Philibert-Ulbéric visant à terme des élections d'une bien plus grande ampleur. Philibert-Ulbéric se demande donc quelle structure de données serait adéquate. Quel est votre avis ?
Quelle structure de données utiliser ?
Une autre structure de données serait préférable pour plus d'efficacité...
Les deux dernières propositions pourraient donc fonctionner, mais les opérations nécessaires seraient très coûteuses à l'usage.
Avec une table de hachage (ou dictionnaire, ou table d'association), nous allons voir qu'il est possible de stocker un nombre quelconque de couples [nom ; numéro de téléphone], par exemple des millions, ... tout en garantissant que les principales opérations (ajout, recherche, ...) sont toujours à coût (amorti) constant, O(1) !
2. Les principes
La structure qui nous manque est la table de hachage.
Le problème de Philibert-Ulbéric se formalise ainsi : nous cherchons à indexer un ensemble de valeurs (les numéros de téléphones) par un ensemble de clés (les noms). Ceci n'est bien sûr pas possible avec un tableau dont les indices sont obligatoirement des entiers (afin d'être capable de calculer l'adresse d'un élément).
Les clés peuvent être n'importe quel objet informatique. Dans le cas simple de Philibert-Ulbéric, les clés sont des chaînes de caractères : les noms des étudiants. Mais la clé peut aussi être un réel - pour l'histogramme des notes des élèves du concours INP par exemple. Cela peut être une structure plus complète contenant par exemple la description complète d'un avion, ou d'un koala.
Les valeurs sont elles aussi n'importe quel objet informatique. Ce sont les données associées à la clé, d'où le nom de table d'association. Dans le cas de Philibert-Ulbéric, les valeurs sont les numéros de téléphone.
Comment rester efficace lorsque l'on recherche les valeurs associées à une clé ? La structure la plus rapide reste le tableau. Nous allons donc y avoir recours. Mais, dans un tableau, les indices sont des entiers. Il faut alors trouver un moyen de transformer une clé en un entier.
Le premier principe essentiel des tables de hachage est de transformer une clé en un entier, qui sera alors l'indice du tableau contenant les données. C'est le rôle de la fonction de hachage, qui assure une correspondance entre notre clé et l'indice entier du tableau.
Dans la suite de cette section, on supposera que nous avons déjà rempli N couples [clés, valeurs] dans notre table d'association.
2.1 Notion de fonction de hachage
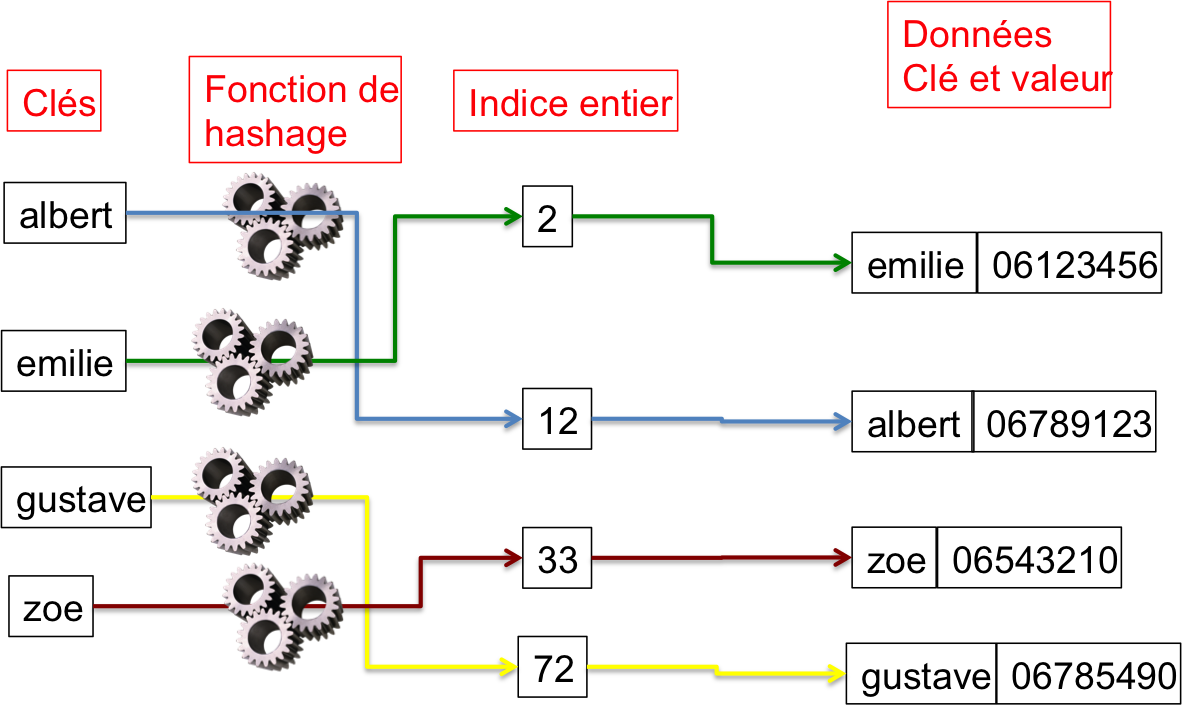
La fonction de hachage est une fonction qui calcule un indice entier à partir d'une clé quelconque. Ainsi, si Philibert-Ulbéric veut construire son annuaire comportant les numéros de téléphones d'albert, émilie, gustave et zoe, le schéma ci dessous illustre les différents éléments à mettre en oeuvre :
- une fonction de hachage qui transforme une clé (un nom) en un indice entier
- un tableau de structures contenant la clé (le nom) et la valeur (le numéro de téléphone) associées à cette clé
2.2 Ajouter un couple clé,valeur dans une table d'association
Laissons Philibert-Ulbéric à ses élections et supposons que nous souhaitions construire un dictionnaire de la langue française. Nous définissons :
- un tableau de M structures contenant deux champs : une chaîne de caractères pour la clé (le mot) et une chaîne de caractères pour la valeur (sa définition),
- une fonction de hachage qui transforme une clé (un mot de la langue française) en un indice entier,
Pour notre 1er exemple, nous choisissons l'algorithme suivant pour la fonction de hachage :hash(mot) = (somme des lettres du mot, avec la correspondance 'a'->1, 'b'->2, .. 'z'->26) modulo M
Comment ajoutons nous des mots et leurs définitions dans la table ?
Pour ajouter un couple [clé, valeur] à une table d'association, il faut donc :
-
calculer l'indice que ce couple occupera dans la table,
c'est à dire exécuter la
fonction de hachagepour récupérer la valeur entière qu'elle retourne ; - placer ce couple [clé, valeur] dans la table à l'indice qui vient d'être calculé
2.3 Rechercher la valeur associée à une clé dans une table d'association
Comment retrouver les informations dans la table, i.e. les définitions des mots ?
Pour rechercher une clé et/ou sa valeur dans une table d'association, il faut donc :
- calculer l'indice que ce couple devrait occuper dans la table, à l'aide de la
fonction de hachage; - s'ils existent, la clé et la valeur sont dans la table, à l'indice qui vient d'être calculé.
2.4 Propriétés essentielles des fonctions de hachage
Dans une table de hachage, la fonction de hachage est utilisée entre autres chaque fois que l'on souhaite ajouter ou rechercher une clé dans la table. Elle doit donc posséder 2 propriétés essentielles :
- la rapidité de calcul : si le temps de calcul de la fonction de hachage est trop long, autant utiliser un tableau tout simple !
- la dispersion : la fonction de hachage doit répartir le mieux possible toutes les valeurs sur l'ensemble des entiers autorisés (0..M-1).
Pour le second point, l'idéal serait une fonction bijective de l'ensemble des clés dans l'ensemble des entiers. Mais ce n'est pas possible.
On retiendra donc que la fonction de hachage :
- doit minimiser les collisions, c'est à dire le cas où des clés différentes donnent la même valeur d'indice (pour les collisions, voir ci dessous)
- doit minimiser les indices (donc les espaces mémoires) inutilisés.
2.5 Exemples de fonctions de hachage
Voici quelques exemples de fonctions de hachage classiques :
- fonction pour les clés alphanumériques : cle est une chaîne de caractères, b est un nombre premier. $$ hash1(cle) = (\sum_{i=0}^{strlen(cle)-1}cle[i]*b^i)\ mod\ M $$
- fonction pour les clés entières : cle est entier. $$ hash3(cle) = cle\ mod\ M $$
- fonction pour les clés réelles : cle est réel. $$ hash4(cle) = partie\ entiere(cle)\ mod\ M $$
3. Hachage et collisions
Reprenons notre dictionnaire et, pour simplifier notre propos, la fonction de hachage simpliste réalisant la somme des lettres de notre clé modulo M.
Que se passe-t-il lorsque l'on veut ajouter le mot male et sa définition ?
Calculons l'indice de hachage à l'aide de la fonction précédente : hash("male")=(13+1+15+5)%100=31
Il faudrait mettre le mot male à l'indice 31 dans la table. Mais voilà : cet indice est déjà occupé par un autre couple clé,définition, celle du mot lame !
C'est ce qu'on appelle une collision.
Une collision se produit chaque fois que la fonction de hachage donne un même indice pour 2 clés différentes.
Les collisions sont dues au fait qu'aucune fonction de hachage n'est une injection de l'espace des clés vers l'espace 0..M-1
Il existe 2 grandes familles de solutions pour gérer les collisions :
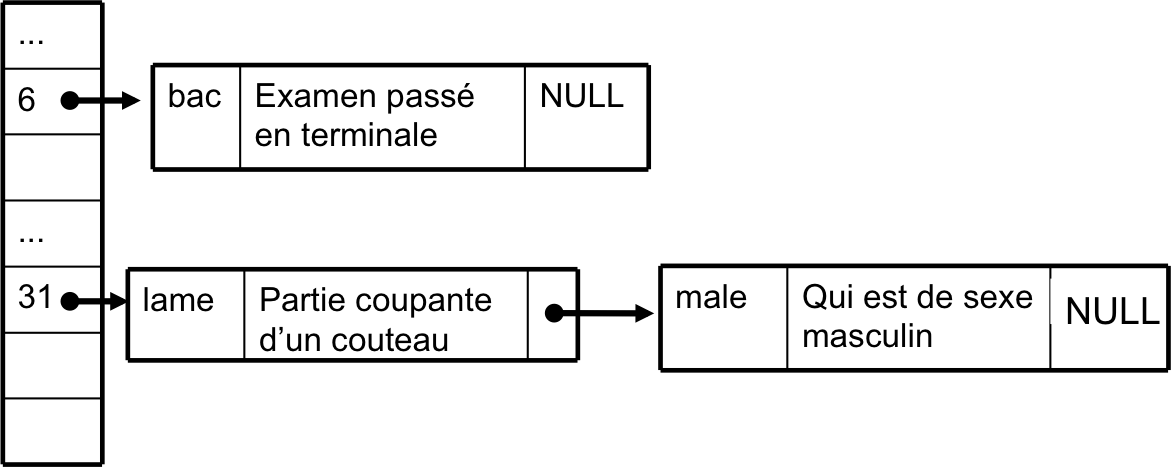
- Le hachage par chaînage : la table sera un tableau de listes chaînées.
Dans les M listes de la table, chaque maillon contient une clé et une définition,
ainsi que l'adresse du maillon suivant.
Pour ajouter un couple clé,valeur à notre table, il suffit d'ajouter
ce couple dans un nouveau maillon, en tête de la liste située à l'indice de hachage.
Ainsi, on apporte bien une solution au problème des collisions !
- Le hachage ouvert : la table est un tableau de M structures avec un champ cle et un champ valeur.
Si une collision apparaît, on recherche une case vide parmi les cases suivantes dans notre table à l'aide d'une fonction de sondage.
La fonction de sondage la plus simple est de choisir la case suivante, puis la suivante, etc... jusqu'à
trouver une case libre.

4. Le TAD hashtable_t
On suppose que les types key_t
et value_t
désignent respectivement le type des clés et le type des valeurs.
On suppose également que le type element_t
est une structure avec les 2 champs contenant les valeurs et clés :
typedef struct {
key_t key;
value_t value;
} element_t;
Interface minimale en C du type abstrait de table d'association :
| prototype | contrat |
|---|---|
hashtable_t hashtable_new(int m) |
crée et retourne une nouvelle table de m listes vides ; |
int hashtable_put(key_t k, value_t v, hashtable_t t) |
ajoute le couple [clé, valeur]
à la table t. Retourne 1 si réussi, 0 sinon ; |
int hashtable_contains(key_t k,hashtable_t t) |
retourne 1 (true) si la clé k existe dans la table, 0 sinon.
|
int hashtable_getvalue(key_t k, value_t* pv, hashtable_t t) |
Recherche la clé k dans la table. Si la clé est présente, remplit la variable pointée par pv avec la valeur associée à la clé et retourne 1. Si la clé n'est pas présente, retourne 0. |
int hashtable_delete_key(key_t k, hashtable_t t) |
Supprime la clé k et la valeur associée de la table t
retourne 1 si la suppression est réalisée, 0 sinon
|
hashtable_t hashtable_delete(hashtable_t t) |
Supprime tous les éléments, détruit la table et retourne une table vide |
void hashtable_print(hashtable_t t) |
Affiche les éléments de la table dans le Terminal. |
5. Hachage par chaînage
La table de hachage est simplement une table de listes chaînées, chaque maillon contenant la clé et la valeur associée.

On utilise les fonctions de base sur les listes pour ajouter en tête, rechercher si une clé est déjà présente, obtenir la valeur associée à une clé, supprimer un couple [clé, valeur].
Remarque : les fonctions et l'interface exposés dans la suite ne sont valables que pour le cas où une clé donnée ne peut pas être présente 2 fois dans la table : une clé n'est associée qu'à une seule valeur.
Le concept s'étend toutefois naturellement au cas où plusieurs valeurs peuvent être associées à une seule clé. On parle alors de "Multi-hashtable". Ceci peut être réalisé au moyen d'une liste de valeurs, au lieu d'une valeur unique.
Voici la définition du type C pour le TAD Hashtable dans le cas du hachage par chaînage :
typedef struct _link {
element_t val; // un élément de la liste
struct _link *next; // l'adresse du maillon suivant
} link_t, *list_t; // les structures de maillon et de liste
typedef struct {
int size; // nombre de listes de la table
list_t* data; // tableau de listes d'éléments, devant être alloué dynamiquement
} hashtable_t; // la structure de la table de hachage
Le type element_t désigne le couple [clé,valeur]. C'est une structure (ou un pointeur sur une structure) contenant une clé et une valeur.
Le type list_t désigne une liste d'éléments.
Le type hashtable_t désigne le TAD table de hachage. C'est une structure contenant la
dimension M de la table et un tableau de M listes, tableau qui sera alloué dynamiquement.
5.1 Création de la table
La fonction hashtable_t hashtable_new(int m) crée une structure et alloue dynamiquement le tableau de listes.
Le code de la fonction est simple :
// Crée et retourne une nouvelle table de m listes vides ;
// Retourne une table vide en cas d'erreur
hashtable_t hashtable_new(int m) {
hashtable_t t;
t.size = 0;
t.data = calloc(m, sizeof(list_t)) ; // allocation du tableau de m listes
if(t.data == NULL) {
return t ; // échec de l'allocation => retourne une table vide
}
t.size = m;
return t;
}
5.2 Insertion d'un couple [clé,valeur]
La fonction int hashtable_put(key_t k, value_t v, hashtable_t t)
ajoute un couple [clé,valeur] par l'algorithme suivant :
h = calculer l'indice de hachage de la clé k.
element_t e = créer un élément contenant la clé k et la valeur v
Ajouter e à la liste d'indice h, c'est à dire à la liste t.data[h]
si l'ajout à la liste a fonctionné
retourner 1
sinon
retourner 0
Attention toutefois : une clé donnée ne doit apparaître qu'une seule fois dans la table ! Pour cela, les implémentations choisissent en général l'une des deux options suivantes :
-
Précondition : le contrat de la fonction
hashtable_put()précise en précondition que la clékne doit pas être déjà présente dans la table. Dès lors, comme d'habitude avec les préconditions, le développeur doit le vérifier avant d'appeler la fonctionhashtable_put(). -
Remplacement : si la clé existe déjà dans la table, alors
la fonction
hashtable_put()remplace la valeur associée par la nouvelle valeur.
Dans cette fiche, on choisit la première option (précondition). Vous verrez la seconde en TD/TP.
Voici alors le code C pour La fonction int hashtable_put(key_t k, value_t v, hashtable_t t) :
/**
Ajoute le couple k,v à la table de hachage t.
retourne 1 si l'ajout est réussi, 0 sinon.
PRECONDITION : k n'est pas une clé déjà existante dans la table
*/
int hashtable_put(key_t k, value_t v, hashtable_t t) {
// Remarque : du fait de la précondition "k n'est pas une clé déjà existante dans la table",
// pas la peine de tester si la clé k existe déjà dans la table.
int h = hash(k, t.size); // calcul du code de hachage pour la clé k
element_t e;
e.key=k;
e.value=v;
/*
Ajout du couple à la liste t.data[i]
Rappel : si l'ajout dans la liste ne réussit pas, list_add_first() retourne l'ancien premier maillon.
Donc il faut d'abord mettre de côté l'ancienne tête de liste.
*/
// 1. On met de côté l'état courant de la liste
list_t old_list=t.data[h];
// 2. tentative d'ajout
t.data[h]=list_add_first(e, t.data[h] );
// 3. On vérifie que l'ajout à la liste s'est bien passé
if (t.data[h] == old_list) {
// Erreur lors de l'ajout
return 0;
}
// Ajout réussi
return 1;
}
5.2 Recherche
La fonction int hashtable_contains(key_t k, hashtable_t t) recherche si la clé est présente par l'algorithme suivant :
h = calculer l'indice de hachage de la clé k
ptr_maillon = valeur de retour de la fonction de recherche de la clé k dans la liste située à l'indice h de la table
si ptr_maillon vaut NULL
retourner 0
sinon
retourner 1
La fonction int hashtable_getvalue(key_t k, value_t* pv, hashtable_t t) recherche si la valeur associée à la clé par l'algorithme suivant :
h = calculer l'indice de hachage de la clé k
ptr_maillon = valeur de retour de la fonction de recherche de la clé k dans la liste située à l'indice h de la table
si ptr_maillon vaut NULL
retourner 0
sinon
*pv = partie valeur du maillon pointée par pmaillon;
retourner 1
5.3 Suppression d'une clé
La fonction int hashtable_deletekey(key_t k, hashtable_t t) supprime la clé (si elle est présente) par l'algorithme suivant
h = calculer l'indice de hachage de la clé k
ptr_maillon = valeur de retour de la recherche de la clé k dans la liste située à l'indice h de la table
si ptr_maillon vaut NULL
retourner 0
sinon
Supprimer le maillon de la liste située à l'indice h de la table;
retourner 1
5.4 Destruction de la table complète
La fonction hashtable_t hashtable_delete(hashtable_t t) supprime tous les éléments et la table par l'algorithme suivant
Pour toutes les listes l de la table t
destruction de la liste l
libérer la mémoire allouée pour le tableau de listes
mettre la taille à 0
retourner t;
6. Hachage ouvert
Le hachage ouvert est une alternative dans laquelle tous les éléments sont stockés dans un tableau, sans listes chaînées.
Il ne peut fonctionner que si le nombre d'éléments de la table est inférieur à la taille de la table.
6.1 Principes du Hachage ouvert et sondage
Pour insérer un couple [clé k, valeur v], on sonde les cases à partir de la case donnée par la fonction de hachage. Cela veut dire qu'on cherche la première case vide à partir de celle d'indice hash(k).
Il existe plusieurs stratégies de sondage :
-
sondage linéaire :
à partir de l'indice j=hash(k), on regarde si la case d'indice j est vide, puis la case j+1, puis j+2, etc jusqu'à trouver une case vide. La fonction de hachage totale s'écrit donc j=hash(k)+i où i est le nombre d'essais.
-
sondage quadratique :
à partir de l'indice j=hash(k), on regarde si la case d'indice j est vide, puis la case j+1, puis j+4, puis j+9 etc jusqu'à trouver une case vide. La fonction de hachage totale s'écrit donc j=hash(k)+c1*i+c2*i*i où j est le nombre d'essais et c1,c2 sont des constantes.
-
sondage double hachage :
on utilise une deuxième fonction de hachage g. A partir de l'indice j=hash(k), on regarde si la case d'indice j est vide, puis la case j+g(k), puis j+2*g(k), etc... jusqu'à trouver une case vide. La fonction de hachage totale s'écrit donc j=hash(k)+i*g(k) où i est le nombre d'essais.
Dans la suite, pour simplifier, les explications s'appuient sur le principe du sondage linéaire.
6.2 Insertion et hachage ouvert
Prenons pour exemple notre fonction de hachage basique (somme des lettres). Voici un exemple d'insertion avec cette fonction et le sondage linéaire.
6.3. Recherche et hachage ouvert
La recherche d'une clé et/ou d'une valeur s'effectue de manière identique. L'algorithme s'écrit de la manière suivante :
i=0
l = calculer l'indice de hachage de la clé k
répéter
h = l + i
si la case h n'est pas vide ET si la clé k est égale à la clé stockée dans la table
alors
retourner la valeur associée à la clé dans la case h
sinon
incrementer i
jusqu'à atteidre une case VIDE ou la fin de la table
retourner "PAS TROUVE"
6.4. Suppression et hachage ouvert
La suppression d'une clé (et de la valeur associée) est un peu plus compliquée. On ne peut pas simplement marquer à VIDE la case du tableau qui contenait la clé.
En effet, si on se contente de vider la case contenant la clé, alors l'algorithme d'insertion et l'algorithme de recherche ne fonctionnent plus. Pour l'expliquer, dans le slide qui suit :
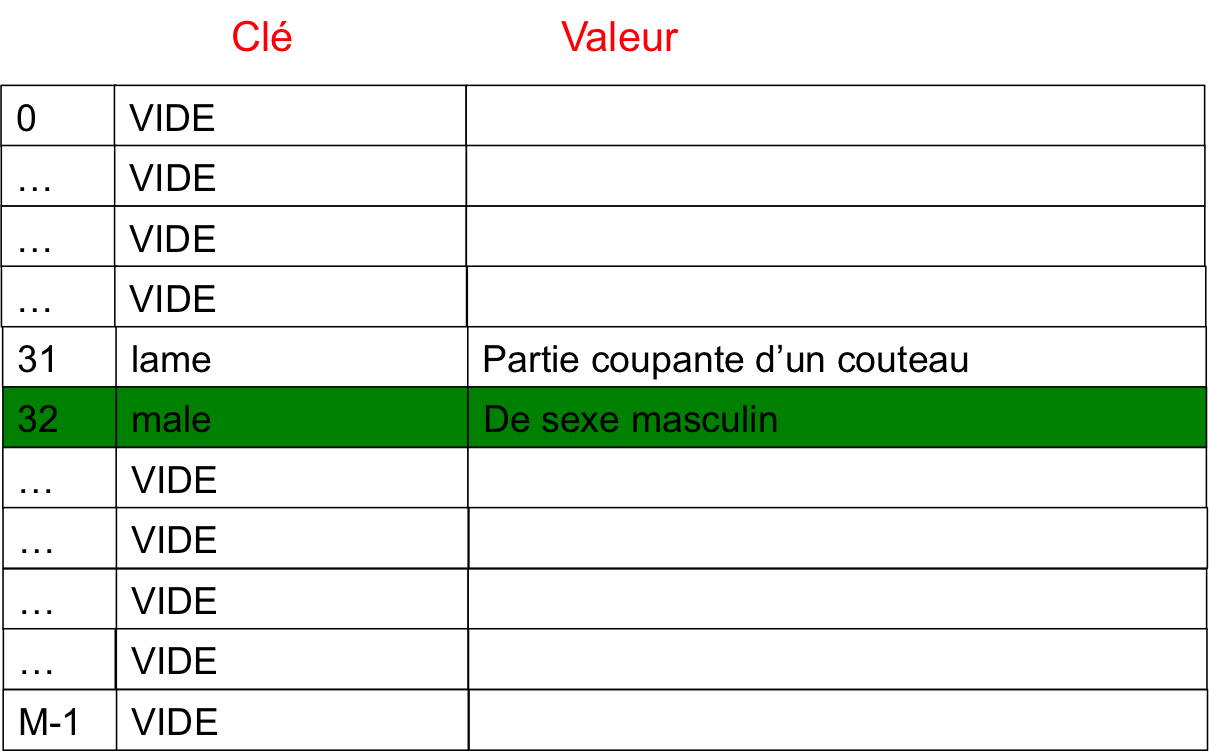
- on ajoute les entrées lame, male, mela, mena dans la table. Les cases d'indice 31 à 34 sont donc remplies.
- puis on supprime l'entrée male avec l'algorithme de suppression erroné qui se contente de vider la case (la case d'incice 32).
L'état de la table est donc à ce moment :

A partir de cet état, dans le slide qui suit, on recherche le mot mela, avec notre algorithme de recherche :
Une solution à ce problème est, dans l'algorithme de suppression, de ne pas vider la case qui contenait la clé supprimée, mais d'indiquer que cette case contenait une clé qui a été supprimée.
Solution pour la suppression d'une clé dans le cas du hachage ouvert :
- on définit une clé spéciale SUPPRIME pour marquer les cases qui sont supprimées.
-
cette clé est utilisée de la manière suivante :
- pour la suppression, on marque la case de la table qui contenait la clé supprimée avec la clé spéciale SUPPRIME.
- pour l'insertion, si on trouve une clé SUPPRIME, on considère cette case comme disponible et on la remplit avec la clé k et la valeur associée.
- pour la recherche, si on trouve une clé SUPPRIME lors de la recherche, on considère cette case comme occupée, mais on passe à l'itération suivante pour le sondage.
Si on implante ainsi l'algorithme de suppression, les deux encarts qui suivent montrent comment il faut modifier les algorithmes d'insertion et de recherche :
// Algorithme corrigé pour linsertion de la la clé k et de sa valeur
i=0
répéter
h = hash(k) + g(k,i)
si la case h est VIDE ou SUPPRIME
alors
remplir cette case avec la clé et sa valeur
sinon
incrementer i
jusqu'à atteidre la fin de la table
Erreur car table pleine
// Algorithme corrigé pour la recherche de la la clé k
i=0
répéter
h = hash(k) + g(k,i)
si la case h n'est pas VIDE
si la case h est SUPPRIME OU si la clé k n'est pas égale à la clé à l'indice h
alors
incrementer i
sinon
retourner la valeur à cet indice h
jusqu'à la case h est VIDE ou la fin de la table est atteinte
retourner PAS TROUVE
Dans ces 2 algorithmes, la fonction g(k,i) est la fonction suivante :
- sondage linéraire : g(k,i) = i
- sondage quadratique : g(k,i) = c1*i+c2*i*i c1 et c2 constantes non nulles
- double hachage : g(k,i) : i*h2(k) où h2 est une deuxième fonction de hachage
7. Comparaison et conclusion
7.1 Complexité moyenne
Les performances dépendent de 2 paramètres :
- la taille de la table M
- le nombre de clés utilisées N
On définit aussi le facteur de charge par α=N/M
| Insertion | Recherche | Suppression | |
|---|---|---|---|
| chaînage | O(1) | O(α) | O(α) |
| linéaire | O(1/(1-α)) | O(1/α . log(1/(1-α))) | O(1/α . log(1/(1-α))) |
Remarque : dans le cas du chaînage linéaire par exemple, tant que la taille M de la table est grande devant le nombre N d'éléments présents dans la table, le facteur de charge α=N/M sera petit (<1).
Dans ce cas, si la fonction de hachage est satisfaisante (peu de collisions), alors toutes les opérations apparaîtront à coût constant O(1)... même s'il y a un très grand nombre (des millions, des milliards...) d'éléments !
7.2 Remarques et comparaison qualitative
Le hachage ouvert par sondage linéaire a l'inconvénient de provoquer des regroupements des clés les unes derrière les autres, provoquant ainsi de nouvelles collisions. C'est le phénomène de grappe.
Exemple avec la fonction de hachage basique (somme des lettres) et le sondage linéaire.
- Ajout de lame, hash=31, indice 31 (car cette case est libre)
- Ajout de male, hash=31, indice 32 (car la case 31 est occupée) : collision classique
- Ajout de mela, hash=31, indice 33 (car les cases 31,32 sont occupées): collision classique
- Ajout de mena, hash=33, indice 34 (car le case 33 est occupée) : collision supplémentaire et grappe
Dans cet exemple, le sondage linéaire introduit une collision inexistante avec la fonction de hachage, puisque le mot mela prend la place du mot mena. Il n'est pas très uniforme.
Le sondage quadratique présente plus rarement ce phénomène de grappe, si les valeurs des constantes c1 et c2 sont bien choisies.
Le sondage par double hachage est plus difficile à implémenter, car la deuxième fonction de hachage devrait être première avec la taille de la table. Il est proche d'une distribution uniforme et meilleur que les 2 précédents.
Le chaînage présente l'inconvénient des listes chaînées. Le coût CPU de l'allocation n'est pas négligeable lors de l'insertion. Les pointeurs pour gérer le chaînage augmentent la taille mémoire nécessaire. De plus, la mémoire tend à être segmentée du fait des listes chaînées, ce qui implique un coût dans la manipulation de la table (parcours par exemple).
7.3 Quel type de hachage choisir ?
- Hachage par chaînage
- Gestion d'un nombre illimité du nombre de clés/valeurs et de collisions
- Performances stables
- Coût de la gestion des listes (mémoire et CPU)
- Adressage ouvert
- Suppression plus difficile
- Rapide et peu coûteux en mémoire
- Nombre de clés/valeurs limité à la taille de la table
- Pour être efficace, il faut que le nombre de clés soit nettement inférieur à la taille de la table (phénomène de grappe). Une partie de la table n'est donc pas utilisée.
 La case d'indice 31 de la table n'est pas vide et contient 2 champs : la clé lame et sa définition
La case d'indice 31 de la table n'est pas vide et contient 2 champs : la clé lame et sa définition
 La case d'indice 6 de la table n'est pas vide et contient la clé bac et sa définition
La case d'indice 6 de la table n'est pas vide et contient la clé bac et sa définition
 La case d'indice 42 de la table est vide et la table ne contient aucune information sur le mot "truc".
La case d'indice 42 de la table est vide et la table ne contient aucune information sur le mot "truc".














La table initiale est vide
hash("bac")=(2+1+3)%100=6
hash("lame")=(12+1+13+5)%100=31