Il existe toute une foule de variations sur le thème des listes !
Pour finir ce chapitre sur le type abstrait Liste, cette fiche décrit brièvement quelques-unes de ces variantes.
Il s'agit de culture générale en informatique et programmation.
1. Implémentation récursive des listes chaînées dynamiques
Les listes sont des structures récursives. On peut les voir comme un élément suivi d'une liste plus petite. Une fonction peut avoir une action sur le premier élément d'une liste non vide, puis appeler récursivement la fonction sur le reste de la liste.
1.1. Parcours sans modification de la liste
Toutes les fonctions qui ne modifient pas la liste peuvent avoir une implémentation récursive du type :
void list_visit_rec( list_t l ) {
if ( ! list_empty( l ) ) {
// Faire qq chose ou pas avec le premier élément l->val
list_visit_rec( l->next );
// Faire autre chose ou pas avec le premier élément l->val
}
else {
// Faire qq chose ou pas si la liste est vide
}
}
Voici un exemple déroulé d'une exécution récursive d'un parcours pour visualiser une liste :
2.2. Parcours avec modification de la liste
Toutes les fonctions qui modifient la liste peuvent avoir une implémentation récursive du type :
list_t list_visit_modify_rec( list_t l ) {
if ( ! list_empty( l ) ) {
// Faire qq chose ou pas avec le premier élément l->val
l->suiv = list_visit_modify_rec( l->next );
// Faire autre chose ou pas avec le premier élément l->val
}
else {
// Faire qq chose ou pas si la liste est vide
}
return l;
}
1.3. Remarque sur les versions récursives des fonctions manipulant les risques
Les versions récursives des fonctions sur les listes sont élégantes, car elles sont une traduction directe de l'expression "une liste est un premier élément et une liste".
Leur complexité algorithmique théorique est la même que la complexité théorique des versions itératives (avec boucle). Par exemple : O(n) pour l'affichage de tous les éléments.
Toutefois, les versions récursives souffrent de 3 limitations :
- Leur complexité pratique est plus grande. En effet, elles s'appuient sur des appels de fonctions, et un appel de fonction est coûteux !
- Leur complexité mémoire est plus grande, car à chaque appel récursif il y a création des variables locales sur la pile d'appel de fonctions.
- Si la liste est (très) grande, elles vont finir par provoquer une erreur de segmentation. En effet, le nombre d'appel récursif possible est limité par la taille de la pile d'appel, déterminée par le système d'exploitation !
Pour ces raisons, on préfère en pratique les versions itératives aux versions récursives, quand bien même ces dernières sont particulièrement élégantes.
2. Listes triées
Les listes triées sont des listes dont les éléments sont ordonnés, quand on les parcourt de manière séquentielle à partir de la tête de la liste : du plus petit au plus grand, ou l'inverse.
Dans une liste triée, l'ordre est établi au moment de l'insertion, et non par un tri ultérieur qui coûterait alors très cher.
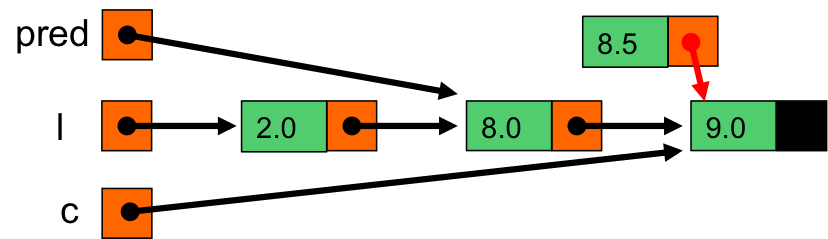
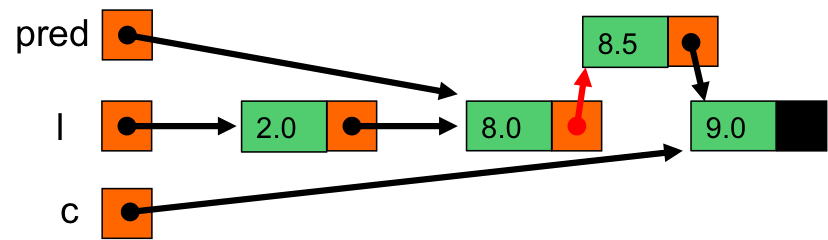
Un nouvel élément est donc inséré entre les deux éléments dont le prédécesseur est plus petit et le successeur est plus grand.
On dénombre donc trois possibilités d'insertion, selon la valeur à insérer dans la liste triée. Par exemple :
- Insérer
2.0dans la liste( 8.0 9.0 )se fait en tête, avant8.0; - Insérer
8.5dans la liste( 8.0 9.0 )se fait entre8.0et9.0; - Insérer
9.5dans la liste( 8.0 9.0 )se fait en queue, après9.0.
2.1. Relation d'ordre sur les éléments
Pour qu'un liste soit triée, il faut bien sur qu'il existe une relation d'ordre sur les éléments placés dans la liste.
En programmation, une relation d'ordre est mise en oeuvre au moyen d'une fonction de comparaison.
Une fonction de comparaison - ou "comparateur" - entre trucs est une fonction qui prend 2 trucs en paramètre pour les comparer. Par convention, un comparateur doit retourner :
0si ces deux trucs sont égaux,- un entier positif si le premier truc est "plus grand" que le second,
- un entier négatif si le premier truc est "plus petit" que le second.
Une telle fonction est nécessaire et suffisante pour implanter une relation d'ordre sur le type des truc.
Le prototype d'une fonction de comparaison est donc :
// Comparateur entre deux variables de type element_t
// Implante une relation d'ordre sur les truc_t
// retourne 0 si a égal b
// retourne un nombre > 0 si a est supérieur à b
// retourne un nombre < 0 si a est inférieur à b
int truc_compare(truc_t a, truc_t b);
Notez que la fonction C int strcmp(const char *s1, const char *s2);
respecte cette convention pour comparer deux chaînes de caractères entre elles
(voir man strcmp).
On va donc ajouter un comparateur
sur le type
element_t des éléments à placer
dans la liste triée, dans le module
element.h /
element.c.
Sa signature est
int element_compare(element_t e1, element_t e2);
// fichier element.h : définition du type d'éléments manipulés
#ifndef ELEMENT_H_
#define ELEMENT_H_
typdef double element_t ; // A ADAPTER au type des élements qu'on veut dans la liste
// Affichage d'un élément
void element_print(element_t e) ;
// Test d'égalité de 2 éléments.
int element_equal(element_t e1, element_t e2);*
// Comparateur.
int element_compare(element_t e1, element_t e2);
#endif
// fichier element.c
#include "element.h"
void element_print(element_t e) {
pritnf("%lf", e); // A ADAPTER au type élément choisi
}
int element_equal(element_t e1, element_t e2) {
return e1 == e2; // A ADAPTER au type élément choisi
}
int element_compare(element_t e1, element_t e2) {
if(e1 == e2){ // A ADAPTER au type élément choisi
return 0;
}
if(e1 > e2) {
return 1;
}
return -1;
}
2.2 Algorithme d'insertion itératif dans une liste triée
L'algorithme d'insertion doit :
- Se positionner sur le maillon précédant le point d'insertion :
- en tête pour insérer
2.0; - sur le maillon contenant
8.0pour insérer8.5; - sur le dernier maillon contenant
9.0pour insérer9.5; - Allouer la mémoire pour le nouveau maillon et mettre la valeur à insérer dans ce maillon ;
- Chaîner le nouveau maillon avec le reste de la liste (
new->next = l) ; - Chaîner le prédécesseur du nouveau maillon avec le nouveau maillon si ce n'est pas une insertion en tête.
Les étapes 2 et 3 peuvent être vues comme l'ajout en tête de la valeur à insérer à la liste commençant après le point d'insertion.
Cela permet de réutiliser la fonction list_add_first.
2.3 Algorithme d'insertion récursive dans une liste triée
Une liste étant une structure récursive, on peut utiliser cette propriété pour l'insertion. L'écriture est alors souvent plus concise qu'avec une version itérative.
L'algorithme pour insérer l'élément e dans la liste l se décrit alors ainsi :
- Si c'est la bonne position (i.e.
econtient un élément plus petit que celui du maillonl) - On retourne la liste obtenue par l'ajout en tete de e à la liste L
- Sinon (on n'est pas au bon endroit pour insérer : il faut avancer récursivement dans la liste)
- On appelle récursivement la fonction pour insérer
esur le reste de la liste. - cette fonction retourne la liste formée par l’ajout de
eau reste de la liste. - Cette nouvelle liste est le nouveau reste de
l - On retourne
l, qui contiente
list_t list_add_sort_rec( element_t e, list_t l ) {
if ( list_empty( l ) || element_compare( e, l->val ) < 0 ) {
return list_add_first( e, l );
}
else {
/* ajouter qqpart apres : la fonction nous renvoie la liste obtenue en ajoutant e
dans le reste de la liste */
l->next = list_add_sort_rec( e, l->next );
return l;
}
}
3. Implémentation des listes basée sur un tableau
Le type abstrait Liste peut être implémenté au moyen d'une structure de donnée basée sur un au moyen d'un tableau de maillons.
Cette implémentation du TAD Liste :
- admet un nombre maximum d'éléments, spécifié au moment de la compilation ;
- ne nécessite pas de gestion mémoire particulière ;
- est donc un peu plus rapide que celle basée sur l'allocation dynamique (cf. infra).
3.1 Description et définition du type C "tableau de maillons"
Note : Cette implémentation n'étant préférable que dans des cas pratiques clairement identifiés, nous la détaillerons moins que celle basée sur l'allocation dynamique, bien plus riche d'enseignements !
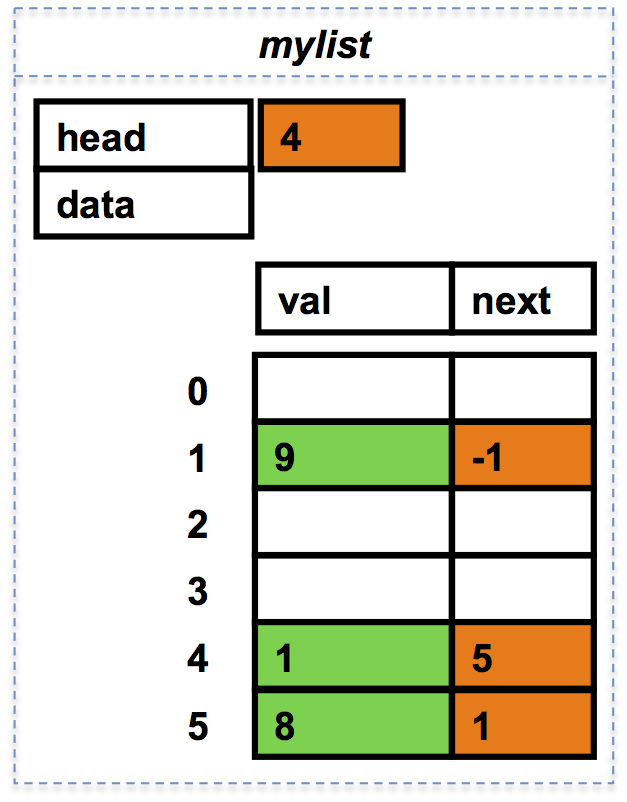
Dans cette implémentation, on utilise un tableau de maillons. De ce fait :
- on repérera donc naturellement un maillon par son indice (de type
int) dans le tableau ; - l'indice "impossible"
-1sera utilisé pour la liste videNIL; - un maillon est constitué :
- d'un
element_tpour l'élément qu'il contient ; - de l'indice entier
nextdu maillon suivant dans le tableau ;
- d'un
- il convient d'ajouter à notre tableau de maillons (appelé
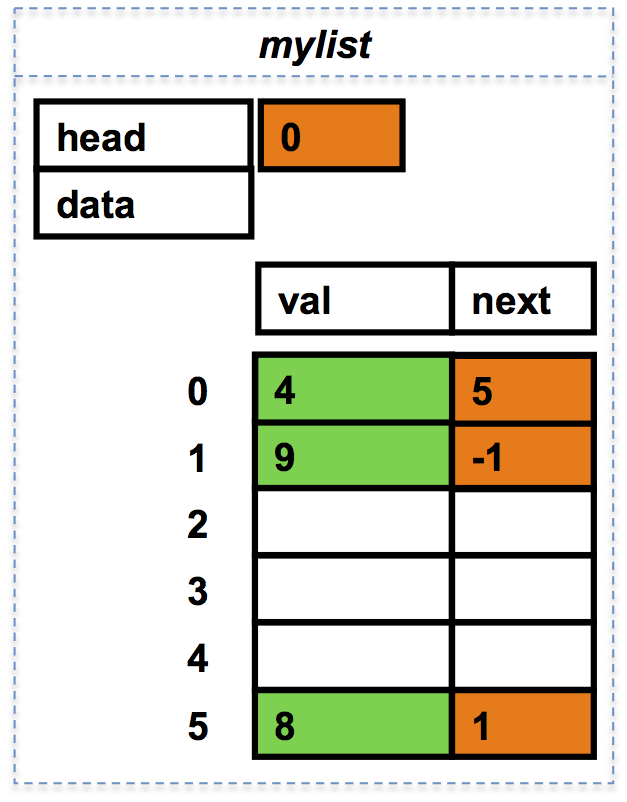
data) l'indiceheadde la tête de liste, le tout formant notre typelist_t.
// list_array.h : liste basée sur un tableau
#ifndef _LIST_ARRAY_H
#define _LIST_ARRAY_H
#include "element.h"
#define LIST_ARRAY_MAX_ELEMENTS 1000
typedef struct {
element_t val;
int next;
} link_t;
typedef struct {
link_t data [ LIST_ARRAY_MAX_ELEMENTS ];
int head;
} list_t;
... //ici : prototype des fonctions du TAD liste
#endif
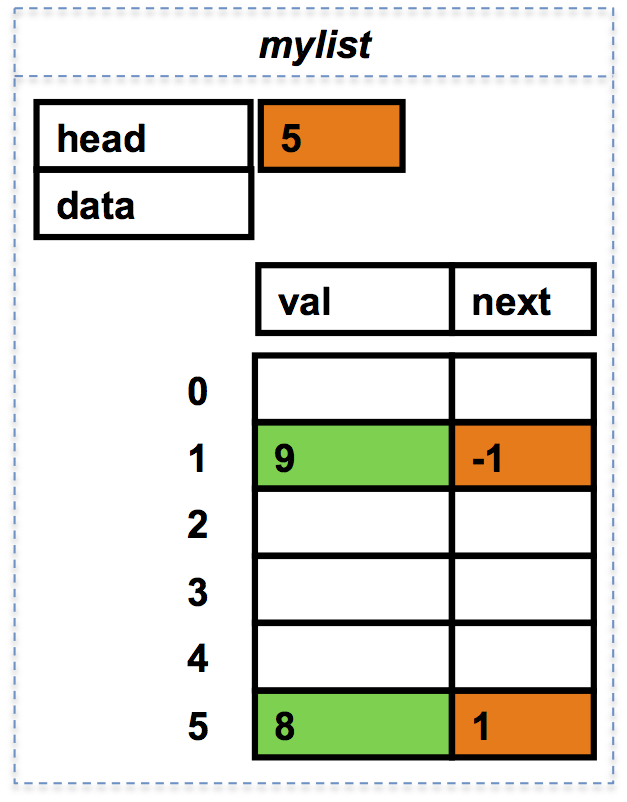
3.2 Implémentation et exemple
Détails d'implémentation :
- on a besoin d'un autre indice "impossible" (
-2) pour marquer le fait qu'un maillon est libre ; - lorsque l'on cherche à effectuer une opération impossible, on quitte le programme en signalant une erreur.
// list_array.c : Implémentation des listes en utilisant un tableau de maillons.
#include "list_array.h"
#define NIL -1
#define EMPTY_LINK -2
list_t list_create() {
list_t l;
int i;
l.head = NIL;
for ( i = 0 ; i < LIST_ARRAY_MAX_ELEMENTS ; i++ ) {
l.data[i].next = EMPTY_LINK;
}
return l;
}
int list_empty( list_t l ) {
return NIL == l.head;
}
size_t list_length( list_t l ) {
size_t len = 0;
int pos = l.head;
while ( NIL != pos ) {
len++;
pos = l.data[ pos ].next;
}
return len;
}
list_t list_del_first( list_t l ) {
assert ( ! list_empty( l ) ) ; // vérification de la précondition "liste non vide"
int new_head = l.data[ l.head ].next;
l.data[ l.head ].next = EMPTY_LINK;
l.head = new_head;
return l;
}
// fonction utilitaire privée
// Retourne l'indice d'un des maillon libre dans le tableau
static int list_array_find_empty_link( list_t l ) {
int i;
for ( i = 0 ; i < LIST_ARRAY_MAX_ELEMENTS; i++ ) {
if ( EMPTY_LINK == l.data[i].next ) return i;
}
return LIST_ARRAY_MAX_ELEMENTS;
}
list_t list_add_first( element_t e, list_t l ) {
int pos = list_array_find_empty_link( l );
if ( pos == LIST_ARRAY_MAX_ELEMENTS ) {
fprintf( stderr, "Fatal: List full, unable to add new element.\n" );
exit( EXIT_FAILURE );
}
l.data[ pos ].val = e;
l.data[ pos ].next = l.head;
l.head = pos;
return l;
}
element_t list_first( list_t l ) {
assert ( ! list_empty( l ) ) ; // vérification de la précondition "liste non vide"
return l.data[ l.head ].val;
}
list_t list_delete( list_t l ) {
return list_new();
}
void list_print( list_t l ) {
printf( "( " );
int pos = l.head;
while ( NIL != pos ){
element_print( l.data[ pos ].val );
printf( " " );
pos = l.data[ pos ].next;
}
printf( ")" );
}
#undef NIL
#undef EMPTY_LINK
4. Autres listes
Il existe toute une foule de variations sur le thème des listes ! Nous ne décrivons ici que les principaux autres types de listes.
-
Dans une liste simplement chainée, il est coûteux de revenir au prédécesseur.
Pour pallier cet inconvénient, on peut définir un pointeur vers le prédécesseur, pour obtenir des listes doublement chainées :

- Les files utilisent le dernier pointeur pour boucler sur le début de la liste afin d'obtenir des listes circulaires :

- Allier circularité et double chaînage donne les listes doublement chainées circulaires :
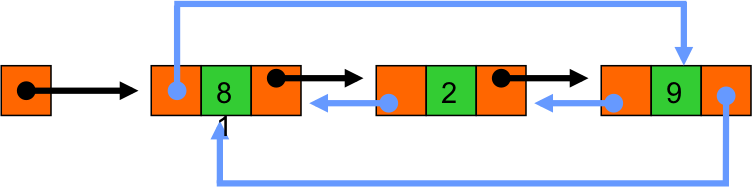
- Les listes triées permettent de maintenir une liste dont les valeurs utiles sont ordonnées à l'insertion :

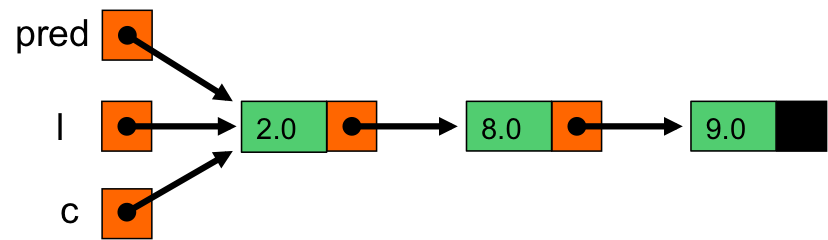
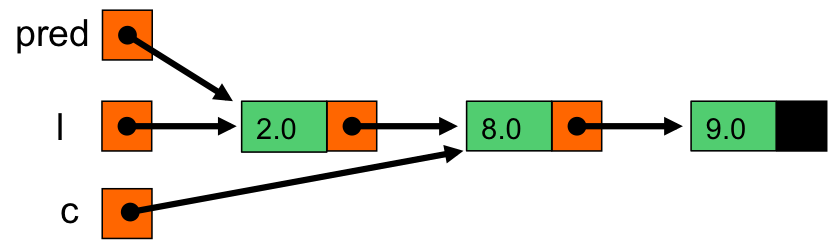
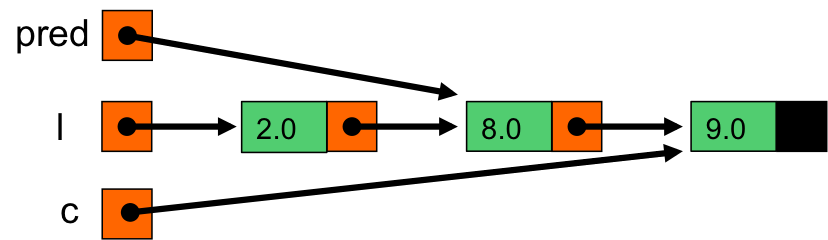
Appel de la fonction d'affichage de la liste {2.0,8.0,9.0}
La liste n'est pas vide !!
L indique le premier maillon, 2.0 dans le contexte;
L non vide;
On affiche
L->val, 2.0 dans le contexte;On execute l'appel récursif;
Mais l'appel de 2.0 n'est pas terminé
L indique le premier maillon, 8.0 dans le contexte;
L non vide;
On affiche
L->val, 8.0 dans le contexte;On execute l'appel récursif;
Mais l'appel de 8.0 n'est pas terminé
L indique le premier maillon, 9.0 dans le contexte;
L non vide;
On affiche
L->val, 9.0 dans le contexte;On execute l'appel récursif;
Mais l'appel de 9.0 n'est pas terminé
L indique la fin de la liste;
Pas d'affichage;
Fin de l'appel récursif (jaune)
Rien à executer ici
Fin de l'appel récursif de 9.0 (bleu)
Rien à executer ici
Fin de l'appel récursif de 8.0 (rouge)
Rien à executer ici
Fin de l'appel récursif de 2.0 (noir)
Fin de l'affichage